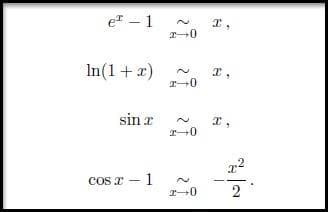Limiti: esercizi svolti

Il calcolo dei limiti è spesso un argomento complesso, soprattutto quando non si ha ben chiaro come procedere nel risolverli!

L’esperienza e l’esercizio sono ottimi alleati per “intuire” quale strada intraprendere.

In questo articolo, ricolveremo alcuni limiti usando il principio di sostituzione degli infinitesimi e lo sviluppo in serie.

$\lim_{x\rightarrow 0}\frac{e^{2x}-1}{ln(1-4x)}$
il numeratore si può approssimare all’esponente mentre il denominatore con -4x, quindi, sostituendo opportunamente, abbiamo un limite equivalente:

$\lim_{x\rightarrow 0}\frac{2x}{-4x}=-\frac{1}{2}$ wow che velocità!
$\lim_{x\rightarrow 0}\frac{1-cosx}{1-cos\frac{x}{2}}$ procedendo con le sostituzioni, si ha: $\lim_{x\rightarrow 0}\frac{\frac{x^2}{2}}{\frac{x^2}{4}\frac{1}{2}}=4$ e come si nota è tutto molto veloce!
$\lim_{x\rightarrow 0}\frac{ln cosx}{\sqrt[4]{1+x^2}-1}$
l’approssimazione, o meglio, la sostituzione da fare è: $\lim_{x\rightarrow 0}\frac{-(1-cosx)}{\frac{x^2}{4}}=\lim_{x\rightarrow 0} \frac{-\frac{x^2}{2}}{\frac{x^2}{4}}=-\frac{4}{2}=-2$
$\lim_{x\rightarrow 0}\frac{cosx-cos2x}{1-cosx}=\lim_{x\rightarrow 0}\frac{-(1-cosx)+1-cos2x}{1-cosx}$
(ho aggiunto e sottratto 1 e messo il meno in evidenza per ricondurmi alla forma voluta, per la sostituzione)

$=\lim_{x\rightarrow 0}\frac{-\frac{x^2}{2}+\frac{4x^2}{2}}{\frac{x^2}{2}}=\lim_{x\rightarrow 0}\frac{\frac{3x^2}{2}}{\frac{x^2}{2}}=3$
$\lim_{x\rightarrow 0}\frac{cosx-1+ \frac{x^2}{2}}{(e^{2x}-2)tgx^4}$
in questo caso non procedo con la sostituzione del coseno, poiché avrei sempre 0 al numeratore. Invece uso lo sviluppo in serie del coseno, utilizzando i primi 3 termini della serie:
$\lim_{x\rightarrow 0}\frac{1-\frac{x^2}{2}+\frac{x^4}{24}-1+\frac{x^2}{2}}{(2x-1)x^4}= \lim_{x\rightarrow 0}\frac{x^4}{24(2x-1)x^4}=-\frac{1}{24}$

Per svolgere i limiti proposti, ho usato queste sostituzioni:

Spero che questi esercizi possano aiutarti a comprendere meglio i limiti

Ora, condividi e lascia un commento. Grazie

A chi potrebbe piacere questo articolo?

Maria Grazia Pastore

E’ consulente all'apprendimento e Docente di Matematica Creativa.

E’ ideatrice del “Metodo MG” per l’apprendimento pratico e facilitato delle materie scolastiche e universitarie.

E’ laureata in matematica indirizzo applicativo, orientamento logico-informatico. Ha svolto la tesi e studi sulla costruzione di curve e superfici nella grafica computerizzata con Open GL.

E’ autrice di diversi ebook e video corsi di matematica e di tecniche di apprendimento per studenti e insegnanti. Scrive per diverse riviste scientifiche e siti. Tra i suoi diversi incarichi ha offerto la sua consulenza ad aziende e professionisti.

Sei stanco di studiare troppo e senza profitto?

Migliora le tue capacità di apprendimento!

Leggi la guida gratuita e scopri come puoi:

Ottenere il tuo metodo di studio efficace;

Velocizzare i tuoi studi con i principi dell’apprendimento "MG";

Organizzare la tua attività di studio per avere più tempo per te;

Avere più risultati nello studio applicando i giusti metodi;

Tornare ad apprezzare la bellezza di apprendere

L’ebook (.pdf) è completamente GRATUITO e si legge velocemente, quindi potrai iniziare subito ad applicare i preziosi consigli. Inserisci la tua email così da ricevere la guida nella tua casella di posta elettronica, inoltre riceverai anche altri nuovi consigli nei prossimi giorni.

NO SPAM! Potrai cancellarti con un click.

Motivi per Preferire Maria Grazia Pastore

Scegliere Maria Grazia Pastore significa affidarsi a professionisti del settore educativo che pongono al centro dell'attenzione la crescita individuale e collettiva degli studenti. Offriamo un approccio didattico innovativo, strutture all'avanguardia e un ambiente inclusivo e stimolante. La nostra missione è fornire un'istruzione di qualità accessibile a tutti, attraverso programmi personalizzati che rispecchiano le capacità e le aspirazioni di ciascun studente. Con un team dedicato e attento alle esigenze di ogni individuo, Maria Grazia Pastore garantisce un percorso formativo eccellente e una solida preparazione per il futuro professionale e personale dei nostri allievi.

Iscriviti alla newsletter

Cookie Policy | Privacy Policy