Dominio di funzioni di due variabili
Come per le funzioni di una variabile reale, anche per quelle in due o pià variabili è necessario e utile studiare il dominio, cioè individaure in quali regioni del piano la funzione è definita.
Per far questo è opportuno ricordare alcune regole generali:
- una funzione razionale fratta non deve avere denominatore nullo;
- radici di indici dispari esistono sempre (tranne per eventuali valori che annullano il denominatore), radici di indice pari esistono per radicando maggiore o uguale a zero;
- la funzione logaritmo esiste quando il suo argomento è positivo (>) e la base è positiva e diversa da 1;
- le funzioni potenza a base reale ed esponente reale esistono quando la base è positiva;
- seno e coseno esitono per ogni x reale; la tangente per
, la cotangente per
;
- arcoseno e arcocoseno sono definite quando l’argomento è compreso tra -1 e 1
(); arcotangente e arcocotangente esistono per ogni x reale.
Bene, come si “traducono” queste condizioni per funzioni in 2 variabili??
Vediamolo con degli esempi!
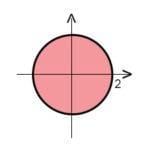
Si tratta di una radice quadrata (indice pari) quindi la Condizione di Esistenza (C.E.) è
L’equazione x2 + y2 =4 rappresenta il cerchio di centro l’origine e raggio 2; poichè a noi serve
, vuol dire che dobbiamo considerare i punti del piano che hanno distanza dall’origine minore del raggio, cioè la parte interna del cerchio, compresa la circonferenza (è minore uguale):
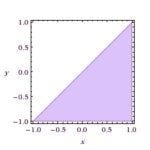
Trattandosi di un logaritmo (base naturale) il suo argomento deve essere positivo:
Osserviamo che x=y è la bisettrice del I-III quadrante e che la regione da considerare è quella formata dai punti la cui ascissa (x) è maggiore dell’ordinata (y): ad esempio, il punto (1,0) soddisfa questa richiesta e tale punto si trova sotto la retta. Questo ci dice che la regione x>y è quella che contiene tale punto, quindi tutta la zona sotto la retta, privata della retta stessa, perché c’è solo la disuguaglianza stretta:La funzione arcocoseno esiste quando l’argomento è compreso tra -1 e 1, quindi per la C.E. imponiamo
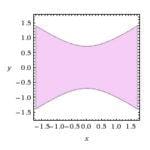
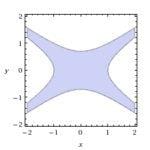
Sono due iperboli, la prima di vertici
e asintoti
; la seconda di vertici
e asintoti
.
Le singole regioni da considerare sono:
che insieme limitano la regione data in figura:
Ovviamente questi sono solo alcuni dei casi che possono presentarsi…
Se hai qualcosa di costruttivo da dire sull’argomento, ti invito a lasciare un commento qui sotto. Clicca mi piace e condividi con le persone che conosci.
Grazie
A chi potrebbe piacere questo articolo?
Maria Grazia Pastore
E’ consulente all'apprendimento e Docente di Matematica Creativa.
E’ ideatrice del “Metodo MG” per l’apprendimento pratico e facilitato delle materie scolastiche e universitarie.
E’ laureata in matematica indirizzo applicativo, orientamento logico-informatico. Ha svolto la tesi e studi sulla costruzione di curve e superfici nella grafica computerizzata con Open GL.
E’ autrice di diversi ebook e video corsi di matematica e di tecniche di apprendimento per studenti e insegnanti. Scrive per diverse riviste scientifiche e siti. Tra i suoi diversi incarichi ha offerto la sua consulenza ad aziende e professionisti.
Sei stanco di studiare troppo e senza profitto?
Migliora le tue capacità di apprendimento!
L’ebook (.pdf) è completamente GRATUITO e si legge velocemente, quindi potrai iniziare subito ad applicare i preziosi consigli. Inserisci la tua email così da ricevere la guida nella tua casella di posta elettronica, inoltre riceverai anche altri nuovi consigli nei prossimi giorni.
NO SPAM! Potrai cancellarti con un click.
