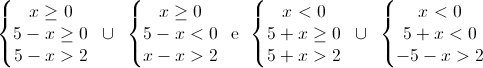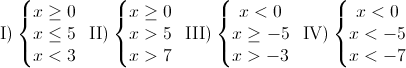Disequazioni con valore assoluto: esercizi svolti

Alcuni studenti trovano difficoltà a svolgere (soprattutto) le disequazioni in valore assoluto, specialmente quando i moduli sono di più oppure annidati. Per questo motivo ho svolto due tipologie di esercizi.
Ricordiamo cosa significa considerare il modulo o valore assoluto di un numero/funzione:
il che equivale a lasciare la quantità racchiusa nel modulo così com’è quando consideriamo la stessa positiva e di cambiarvi il segno quando valutiamo il caso negativo.
I) Risolviamo il seguente esercizio:
i due valori assoluti presenti si “influenzano” a vicenda. Difatti, dovremmo considerare i casi in cui sono entrambi positivi, entrambi negativi, uno positivo e l’altro negativo.
Ma questo si “traduce” brevemente dicendo che sono concordi (positivo/positivo o negativo/negativo) o discordi (positivo/negativo o negativo/positivo).
Come calcolarlo??
Con lo studio del segno! Quindi, seguiamo questa strada di risoluzione:
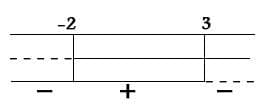
il cui grafico risolutivo è:
Allora i casi da studiare sono tre: quando x è compresa tra -2 e 3, quando è minore di -2 e quando è maggiore di 3.
Allora, risolvendo abbiamo:
Ci resta solo da trovare la soluzione finale e la otterremo unendo (in accordo col simbolo usato tra i sistemi) le soluzioni intermedie trovate. In definitiva, la disequazione è risolta per x<1/2.
II) Risolviamo il seguente esercizio:
E’ evidente che non possiamo sciogliere il modulo esterno se prima non risolviamo quello interno, perciò si inizia da quello più interno. Abbiamo compreso che la distinzione è sempre la stessa, quando -cioè- la quantità contenuta nel valore assoluto è positiva o negativa. Otteniamo i primi sistemi partendo da |x|:
Ed ora dobbiamo fare la distinzione per i moduli rimasti: per x positivo o nullo, dobbiamo considerare (5-x) una volta positivo ed una volta negativo; per x negativo, dobbiamo considerare (5+x) una volta positivo ed una negativo. Pertanto avremo:
Risolviamo ordinatamente i sistemi ottenuti:
- Il sistema (I) è soddisfatto per 0<x<3, 0 incluso;
- il (II) per x>7;
- il (III) per -3<x<0;
- il (IV) per x<-7
L’unione di tutte queste soluzioni ci dà quella definitiva per la disequazione di partenza, ed è
P.S. Sarò lieta di rispondere alle tue domande e ti sarò grata se mi segnalerai eventuali errori che possono sempre capitare… ![🙂]()
A chi potrebbe piacere questo articolo?

Maria Grazia Pastore
E’ consulente all'apprendimento e Docente di Matematica Creativa.
E’ ideatrice del “Metodo MG” per l’apprendimento pratico e facilitato delle materie scolastiche e universitarie.
E’ laureata in matematica indirizzo applicativo, orientamento logico-informatico. Ha svolto la tesi e studi sulla costruzione di curve e superfici nella grafica computerizzata con Open GL.
E’ autrice di diversi ebook e video corsi di matematica e di tecniche di apprendimento per studenti e insegnanti. Scrive per diverse riviste scientifiche e siti. Tra i suoi diversi incarichi ha offerto la sua consulenza ad aziende e professionisti.

Sei stanco di studiare troppo e senza profitto?


Migliora le tue capacità di apprendimento!
L’ebook (.pdf) è completamente GRATUITO e si legge velocemente, quindi potrai iniziare subito ad applicare i preziosi consigli. Inserisci la tua email così da ricevere la guida nella tua casella di posta elettronica, inoltre riceverai anche altri nuovi consigli nei prossimi giorni.

NO SPAM! Potrai cancellarti con un click.